– Per Fernando Blasco –
Aquesta Ruta Matemàgica per Santa Cristina d’Aro us proposa 8 jocs que poden semblar molt màgics, però que de fet són molt matemàtics. Anem a veure com funciona cadascun.
Joc 1: Anem on anem, anem on volem?
Trieu una paraula qualsevol, i després us moveu on voleu, en qualsevol direcció… i aneu a parar sempre a la mateixa paraula final, feu el que feu!
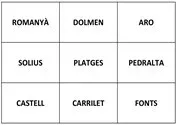
En aquest joc mana un principi de paritat: les caselles numerades així:
123 (1 ROMANYÀ – 2 DOLMEN – 3 ARO )
456 (4 SOLIUS – 5 PLATGES – 6 PEDRALTA)
789 ( 7 CASTELL – 8 CARRILET – 9 FONTS)
porten a aquest esquema:
SPS : Senar Parell Senar
PSP: Parell Senar Parell
SPS: Senar Parell Senar
Fixeu-vos que el nombre de lletres dels mots de cada casella tenen la mateixa paritat que la casella on es troben. Per exemple, “Solius” és a la casella 4 (nombre Parell) i té 6 lletres (nombre també Parell). Per tant, després de situar-nos en una casella i moure’ns per primera vegada, sempre acabarem en una casella Parell, i per tant podem tatxar una Senar (això és deu a que Parell + Parell dóna sempre un nombre Parell, i que Senar + Senar també dóna un nombre parell). A partir d’aquí sempre ens movem un nombre Senar de moviments (les instruccions us diuen: “Moveu 9 caselles”, “Moveu 7 caselles…”), així que alternativament anirem a parar a caselles Senar, Parell, Senar…. (Parell + Senar = Senar, però Senar + Senar= Parell) i haurem de tatxar les oposades.
Joc 2: El quadrat misteriós

Aquí us presentem una matriu de 4 files i 4 columnes, amb 16 números, i us demanem que trieu un número qualsevol, l’encercleu i que tatxeu els altres números de la seva mateixa fila i columna. Repetint l’operació dos cops més us quedaran 4 números encerclats, i sumant-los dona sempre la mateixa quantitat, 46, malgrat que heu triat els números que heu volgut. Com pot ser?
El truc es basa en el fet que les files 2, 3 i 4 s’obtenen al sumar 5, 2 i 6, respectivament, als elements de la primera fila. Ho podeu comprovar: 13 és 8 + 5, 10 és 8+2, etcètera. El procés d’envoltar un número amb un cercle i de tatxar els altres elements que estan sobre la mateixa fila i columna ens porta a un esquema en que cada fila i cada columna es considera una única vegada. Per tant, la SUMA TOTAL serà la suma dels elements de la primera fila més 5, 2 i 6, independentment de com triem els números de la matriu.
Joc 3: L’art de dominar el temps
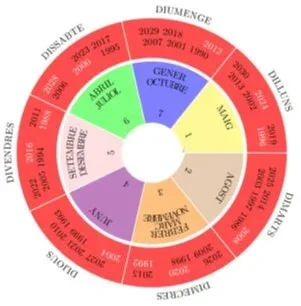
Aquest joc es basa en un mètode ideat per Lewis Carroll, l’autor d’Alicia en el País de les Meravelles, per a calcular el dia de la setmana. El primer moviment, el número del any, determina en quin dia de la setmana va acabar l’any anterior. Per exemple, el 2020 va acabar en dijous, i per això el número associat al 2021 és el 4. Els números associats a cada mes són el desfasament produït al mes anterior. Per exemple, al febrer se li associa el 3 per que gener té 4 setmanes complertes més tres dies (per a completar els 31 dies). Per últim, el dia del mes suposa avançar en el calendari. Totes aquestes dades, sumades, fan que avancem en el calendari un determinat nombre de dies. Però “el vuitè dia de la setmana” és, de nou, un dilluns, i per tant es pot comptar donant voltes al cercle, de la mateixa manera que a un rellotge les 18h apareixen al mateix lloc que les 6. Aquesta idea es coneix com “aritmètica modular” i té moltes aplicacions. Aquesta adaptació de la idea de Lewis Carroll, feta per comptar amb els dits, va ser pensada per primer cop per Fernando Blasco i Miquel Duran específicament per a aquest projecte de ruta matemàgica.
Joc 4: Quan l’ordre emergeix del desordre
Heu escrit a uns números a uns papers, els heu mogut com heu volgut…. i sempre surt la mateixa suma final! Com pot ser? El principi matemàtic que s’amaga sota aquest joc s’assembla al del joc número 2: si ens hi fixem, veurem que la diferència entre els números escrits a cada cara del mateix paper sempre és 146. Les instruccions que es donen dificulten seguir les operacions, però en realitat, al final, dos dels quatre papers queden mostrant el major dels números que tenen, i els altres dos ensenyant el menor. Així, el total ha de ser la suma dels 4 números menors (de cada paper) més 2 vegades la diferència. Això sempre dóna com a resultat 1855.
Joc 5: Atzar, romans i monedes d’euro
Aquí heu bellugat 3 monedes a l’atzar… i el joc ha predit on era cadascuna en acabar els moviments. Tot plegat també es basa en un principi bàsic que queda ocult darrera les instruccions donades. En un dels primers passos, sense adonar-nos-en, s’indica que es bellugui la de 10 cèntims a la dreta, i després la d’un euro a l’esquerra. A partir d’aquest punt tot queda ja determinat. En matemàtiques moltes vegades passen coses similars: hi ha operacions (o expressions, simplificacions…) que se’ns passen desapercebudes però tenen molta importància per al correcte desenvolupament d’un problema.
Joc 6: De mot a mot, hi arribo fent un bot
Salteu de paraula en paraula d’un poema, i tot i que heu decidit per quina comenceu, acabeu sempre al mateix lloc! Aquest joc és una idea del físic Martin D. Kruskal. El joc es basa en el fet que, independentment de la paraula per la qual comencem, la seqüència de paraules en les que anem caient se solaparà amb una seqüència diferent i, per tant, a partir d’un cert moment l’evolució de les dues cadenes serà la mateixa. Es tracta d’un joc de probabilitats: amb un text triat a l’atzar hi ha una alta probabilitat que, començant per on sigui, s’arribi a la mateixa paraula final. Però no sempre passa. Si augmentem la longitud del text, la probabilitat augmenta.
Joc 7: La clau del tresor
Aquest joc és un problema lògic de Raymond Smullyan, un matemàtic que es va dedicar, entre d’altres coses, a la lògica. Smullyan és autor de molts llibres d’introducció a la lògica de forma amena. També era aficionat a la màgia, l’humor i la música. De fet es va pagar els estudis de matemàtiques fent actuacions a diverses sales d’espectacles. Dit això, la millor manera de resoldre aquest problema és seguir un raonament heurístic: això vol dir anar cas per cas veient què passaria si el tresor hi fos en aquell cofre i comprovant si aquesta possibilitat és consistent amb els cartells dels cofres. Als llibres de Smullyan hi ha molts exercicis en aquesta línia.
Joc 8: Fi de festa a la casa màgica
Tornem a trobar-nos amb un principi “de punt fixe”. Encara que no ho sembli, la distància que hi ha entre la carta triada i la carta que esta girada és sempre de 2 cartes. Això permet controlar la seva posició, i les instruccions finals fan que aquesta carta hi romangui i les dues que hi són al costat es girin. Sembla màgia però és un procés completament controlat (la qual cosa, segons com es miri, també és màgica J)